3MC Course on Epidemiological Modelling

Logo

Course material (slides and code).

View the Project on GitHub julien-arino/3MC-course-epidemiological-modelling

Stochastic epidemic models

6 April 2022

Julien Arino width:32px width:32px width:32px

Department of Mathematics & Data Science Nexus University of Manitoba*

Canadian Centre for Disease Modelling Canadian COVID-19 Mathematical Modelling Task Force NSERC-PHAC EID Modelling Consortium (CANMOD, MfPH, OMNI/RÉUNIS)

* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.

Outline

Remarks / Resources

This is a user-oriented course: I barely, if at all, touch on the algorithms; instead, I focus on how to use them

Code is available in this Github repo in the CODE directory

Some of the slides are inspired from slides given to me by Linda Allen (Texas Tech). I recommend books and articles by Linda for more detail

Why stochasticity matters

Running example - SIS model without demography

Constant total population $P^\star$

width:400px

Basic reproduction number: \(\mathcal{R}_0 = \dfrac{\beta}{\gamma}P^\star\)

In the deterministic world, $\mathcal{R}_0$ rules the world

Next slides: $P^\star = 100$K, $\gamma=1/5$, $\mathcal{R}_0={0.8,1.5,2.5}$ (and $\beta=\gamma \mathcal{R}_0/P^\star$)

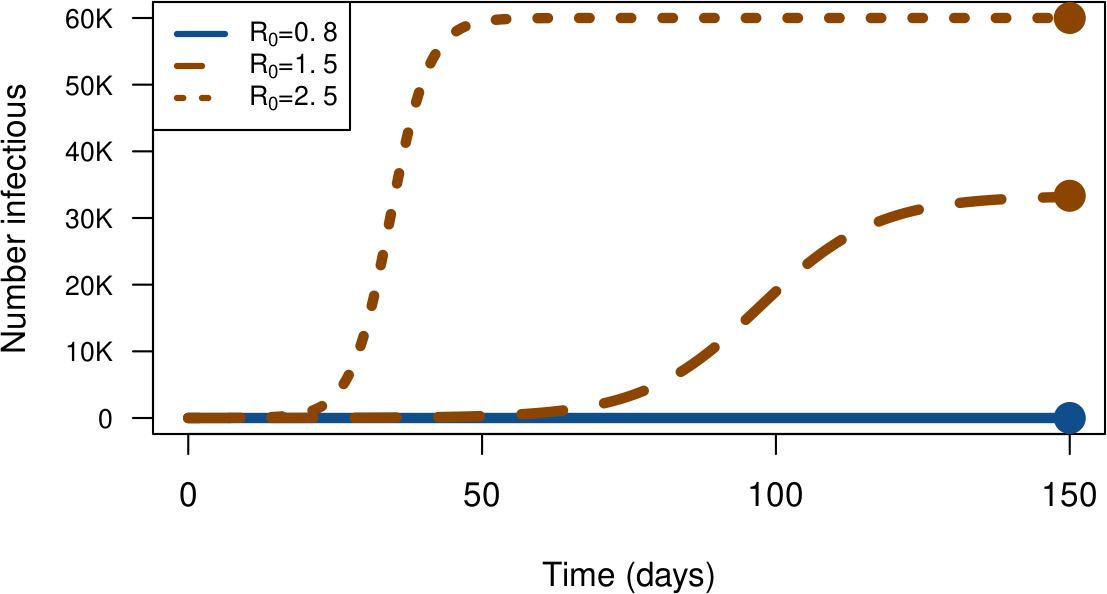
bg contain

In stochastic world, make that ‘’$\mathcal{R}_0$ rules-ish’’ ($\mathcal{R}_0=1.5$)

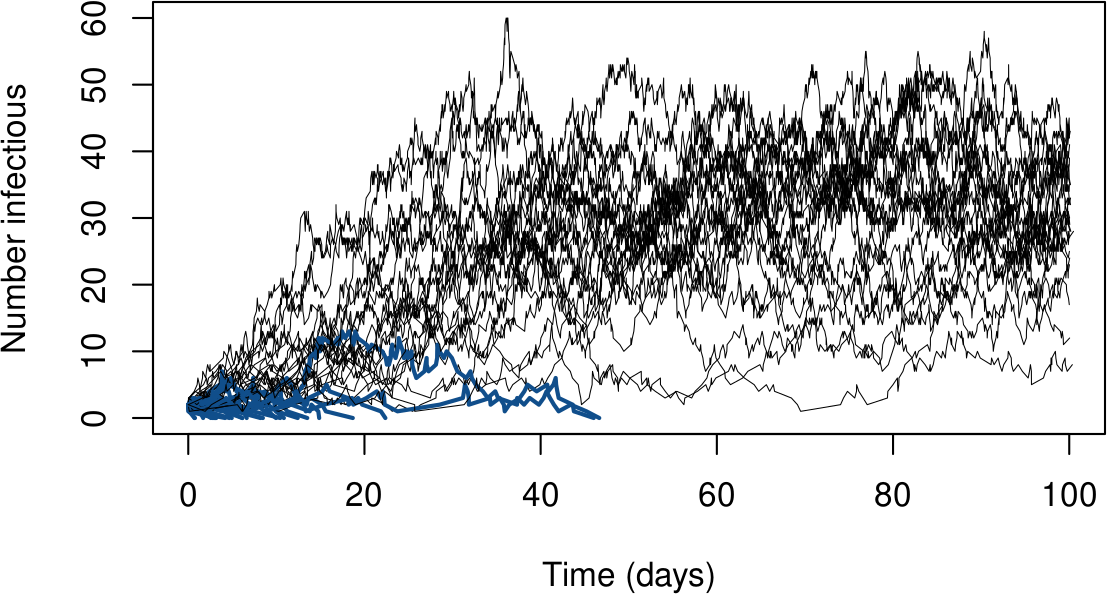
height:600px center

When $I_0=2$, extinctions happen quite frequently

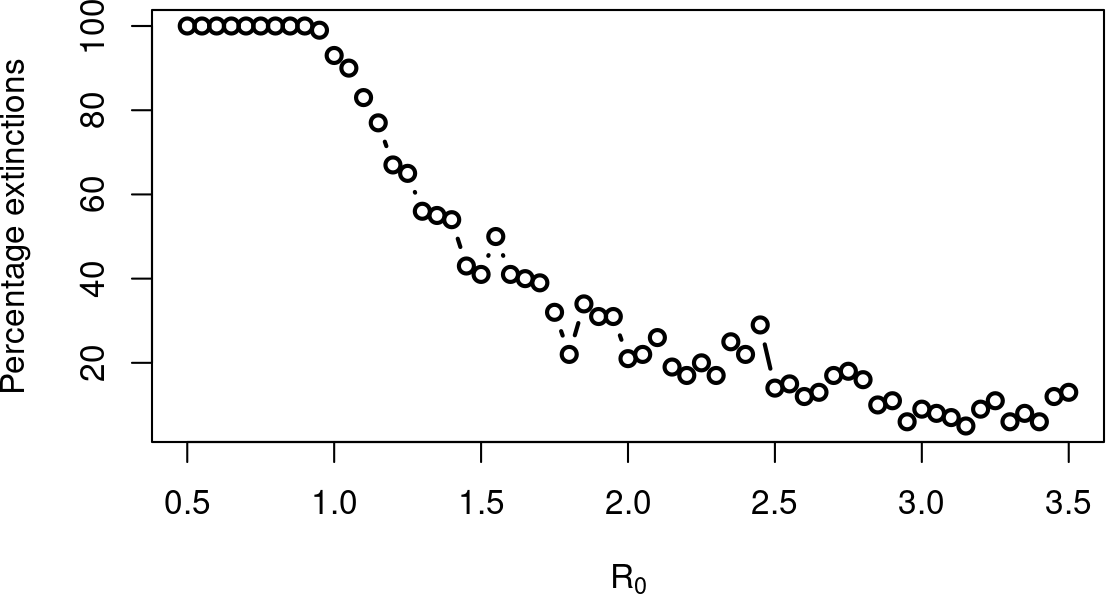
height:600px

Types of stochastic systems discussed today

But there are many others. Of note:

Discrete time Markov chains

Discrete-time Markov chains

$p(t)=(p_1(t),\ldots,p_n(t))^T$: probability vector, with $p_i(t)$ describing the probability that at time $t$, the system is in state $S_i$, $i=1,\ldots,n$

$\sum_i p_i(t)=1$ for al# l $t$, of course

State evolution governed by \(p(t+\Delta t) = A(\Delta t)p(t)\) where $A(\Delta t)$ is a stochastic matrix (row sums all equal 1), the transition matrix, with entry $a_{ij}=\mathbb{P}(X_{t+\Delta t}=s_i|X_t=s_j)$, where $X_1,\ldots$ sequence of random variables describing the state

If $A(\Delta t)=A$ constant, homogeneous DTMC

Time often ‘‘recast’’ so that $\Delta t=1$

Important remark

The DTMC world lives at the interface between probabilists, who like to think of $p(t)$ as a row vector, $A(\Delta t)$ as a column-stochastic matrix and thus write \(p(t+\Delta t) = p(t)A(\Delta t)\) and linear algebraists, who prefer column vectors and row-stochastic matrices, \(p(t+\Delta t) = A(\Delta t)p(t)\)

So check the direction to understand whether you are using $A$ or $A^T$

Advantages of DTMC

As a teacher of modelling: base theory of DTMC uses a lot of linear algebra and graph theory; usually really appreciated by students

Regular DTMC (with primitive transition matrices) allow to consider equilibrium distribution of probability

Absorbing DTMC (with reducible transition matrices) allow the consideration of time to absorption, mean first passage time, etc.

See for instance book of Kemeny and Snell

DTMC for example SIS system

Since $S=P^\star-I$, consider only the infected. To simulate as DTMC, consider a random walk on $I$ ($\simeq$ Gambler’s ruin problem)

Denote $\lambda_I = \beta (P^\star-I)I\Delta t$, $\mu_I = \gamma I\Delta t$ and $\sigma_I=1-(\lambda_I+\mu_I)\Delta t$

width:1200px

Transition matrix

\[A = \begin{pmatrix} 1 & 0 \\ \mu_1 & \sigma_1 & \lambda_1 & 0 \\ 0 & \mu_2 & \sigma_2 & \lambda_2 & 0 \\ \\ & & & & & \ddots \\ \\ & & & & & & 0 & \mu_{P^\star-1} & \mu_{P^\star-1} & \lambda_{P^\star-1} & 0 \\ &&&&&&&& 0 & \mu_{P^\star} & \sigma_{P^\star} \end{pmatrix}\] 
# Make the transition matrix
T = mat.or.vec(nr = (Pop+1), nc = (Pop+1))
for (row in 2:Pop) {
  I = row-1
  mv_right = gamma*I*Delta_t # Recoveries
  mv_left = beta*I*(Pop-I)*Delta_t # Infections
  T[row,(row-1)] = mv_right
  T[row,(row+1)] = mv_left
}
# Last row only has move left
T[(Pop+1),Pop] = gamma*(Pop)*Delta_t
# Check that we don't have too large values
if (max(rowSums(T))>1) {
  T = T/max(rowSums(T))
}
diag(T) = 1-rowSums(T)

Simulating a DTMC

library(DTMCPack)
sol = MultDTMC(nchains = 20, tmat = T, io = IC, n = t_f)

gives 20 realisations of a DTMC with transition matrix T, initial conditions IC (a vector of initial probabilities of being in the different $I$ states) and final time t_f

See code on Github

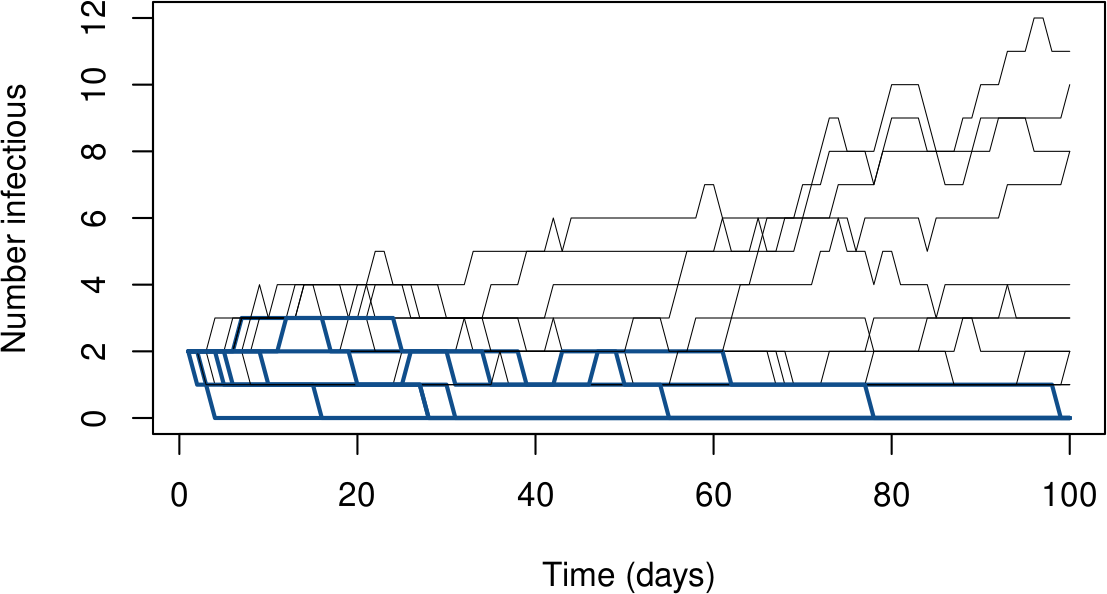
bg contain

Going a bit further

DTMCPack is great for obtaining realisations of a DTMC, but to study it in more detail, markovchain is much more comprehensive

library(markovchain)
mcSIS <- new("markovchain", 
             states = sprintf("I_%d", 0:Pop),
             transitionMatrix = T,
             name = "SIS")

Note that interestingly, markovchain overrides the weird default “* is Hadamard, %*% is usual” R matrix product rule, so mcSIS*mcSIS does $TT$, not $T\circ T$

> summary(mcSIS)
SIS  Markov chain that is composed by: 
Closed classes: 
I_0 
Recurrent classes: 
{I_0}
Transient classes: 
{I_1,I_2,I_3,I_4,I_5,I_6,I_7,I_8,I_9,I_10,I_11,I_12,I_13,I_14,I_15,
I_16,I_17,I_18,I_19,I_20,I_21,I_22,I_23,I_24,I_25,I_26,I_27,I_28,
I_29,I_30,I_31,I_32,I_33,I_34,I_35,I_36,I_37,I_38,I_39,I_40,I_41,
I_42,I_43,I_44,I_45,I_46,I_47,I_48,I_49,I_50,I_51,I_52,I_53,I_54,
I_55,I_56,I_57,I_58,I_59,I_60,I_61,I_62,I_63,I_64,I_65,I_66,I_67,
I_68,I_69,I_70,I_71,I_72,I_73,I_74,I_75,I_76,I_77,I_78,I_79,I_80,
I_81,I_82,I_83,I_84,I_85,I_86,I_87,I_88,I_89,I_90,I_91,I_92,I_93,
I_94,I_95,I_96,I_97,I_98,I_99,I_100}
The Markov chain is not irreducible 
The absorbing states are: I_0

Function Role
absorbingStates absorbing states of the transition matrix, if any
steadyStates the vector(s) of steady state(s) in matrix form
meanFirstPassageTime matrix or vector of mean first passage times
meanRecurrenceTime vector of mean number of steps to return to each recurrent state
hittingProbabilities matrix of hitting probabilities for a Markov chain
meanAbsorptionTime expected number of steps for a transient state to be absorbed by any recurrent class
absorptionProbabilities $\mathbb{P}$ transient states being absorbed by each recurrent state
canonicForm canonic form of transition matrix
period the period of an irreducible DTMC
summary DTMC summary

</span>

Continuous time Markov chains

Continuous-time Markov chains

CTMC similar to DTMC except in way they handle time between events (transitions)

DTMC: transitions occur each $\Delta t$

CTMC: $\Delta t\to 0$ and transition times follow an exponential distribution parametrised by the state of the system

CTMC are roughly equivalent to ODE

ODE to CTMC : focus on different components

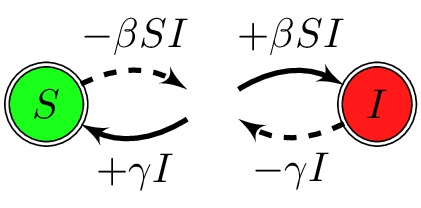
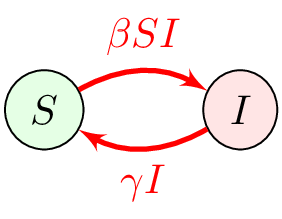
width:600px width:400px

Weight Transition Effect
$\beta SI$ $S\to S-1$, $I\to I+1$ new infection of a susceptible
$\gamma I$ $S\to S+1$, $I\to I-1$ recovery of an infectious

Will use $S=N^*-I$ and omit $S$ dynamics

Gillespie’s algorithm (SIS model with only I eq.)

set $t\leftarrow t_0$ and $I(t)\leftarrow I(t_0)$ while {$t\leq t_f$}

You can also use a package

Simulating a CTMC

library(GillespieSSA2)
IC <- c(S = (Pop-I_0), I = I_0)
params <- c(gamma = gamma, beta = beta)
reactions <- list(
  reaction("beta*S*I", c(S=-1,I=+1), "new_infection"),
  reaction("gamma*I", c(S=+1,I=-1), "recovery")
)
set.seed(NULL)
sol <- ssa(
    initial_state = IC,
    reactions = reactions,
    params = params,
    method = ssa_exact(),
    final_time = t_f,
)
plot(sol$time, sol$state[,"I"], type = "l",
     xlab = "Time (days)", ylab = "Number infectious")

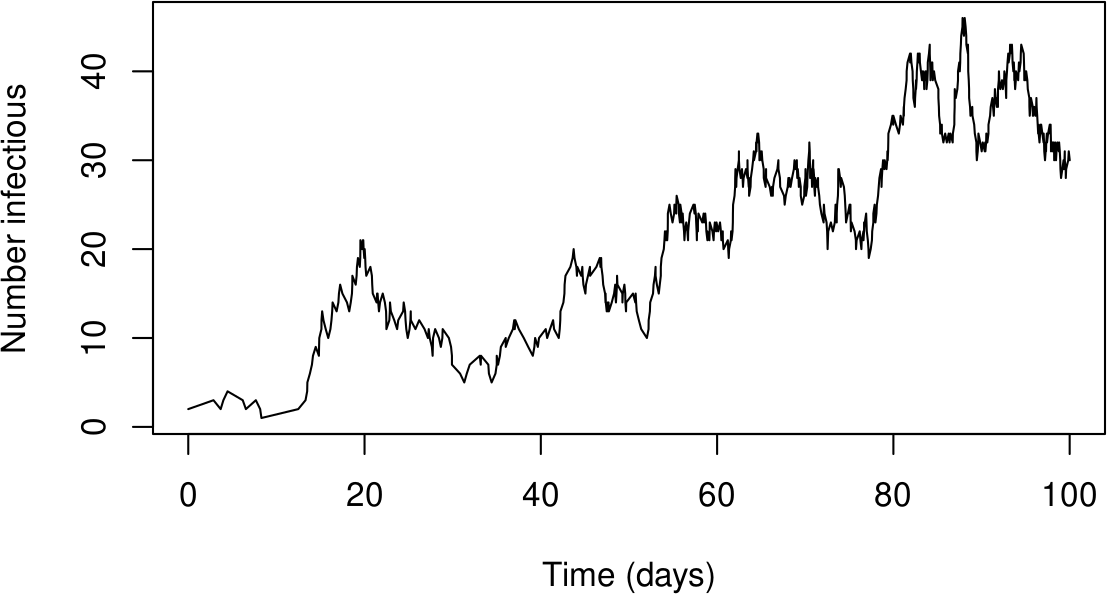
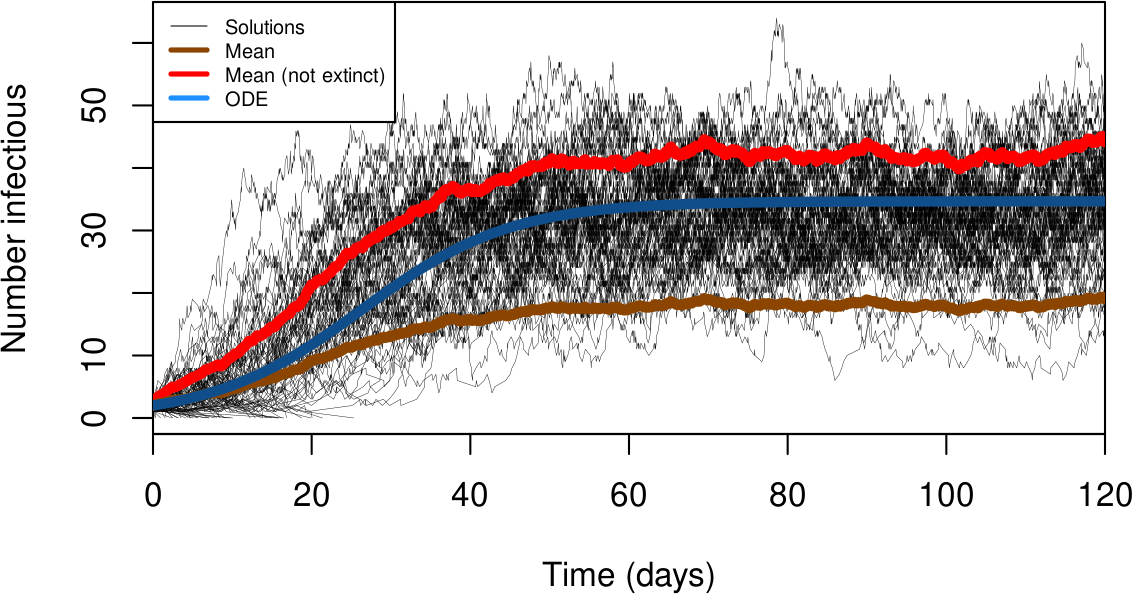
bg contain

bg contain

Sometimes in a CTMC things go bad

Example: a birth and death process

Gillespie’s algorithm (birth-death model)

set $t\leftarrow t_0$ and $N(t)\leftarrow N(t_0)$ while {$t\leq t_f$}

b = 0.01   # Birth rate
d = 0.01   # Death rate
t_0 = 0    # Initial time
N_0 = 100  # Initial population

# Vectors to store time and state. Initialise with initial condition.
t = t_0
N = N_0

t_f = 1000  # Final time

# We'll track the current time and state (could also just check last entry in t
# and N, but will take more operations)
t_curr = t_0
N_curr = N_0

while (t_curr<=t_f) {
  xi_t = (b+d)*N_curr
  # The exponential number generator does not like a rate of 0 (when the 
  # population crashes), so we check if we need to quit
  if (N_curr == 0) {
    break
  }
  tau_t = rexp(1, rate = xi_t)
  t_curr = t_curr+tau_t
  v = c(b*N_curr, xi_t)/xi_t
  zeta_t = runif(n = 1)
  pos = findInterval(zeta_t, v)+1
  switch(pos,
         { 
           # Birth
           N_curr = N_curr+1
         },
         {
           # Death
           N_curr = N_curr-1
         })
  N = c(N, N_curr)
  t = c(t, t_curr)
}

Drawing at random from an exponential distribution

If you do not have an exponential distribution random number generator.. We want $\tau_t$ from $T\thicksim\mathcal{E}(\xi_t)$, i.e., $T$ has probability density function \(f(x,\xi_t)= \xi_te^{-\xi_t x}\mathbf{1}_{x\geq 0}\) Use cumulative distribution function $F(x,\xi_t)=\int_{-\infty}^x f(s,\xi_t)\,ds$ \(F(x,\xi_t)= (1-e^{-\xi_t x})\mathbf{1}_{x\geq 0}\) which has values in $[0,1]$. So draw $\zeta$ from $\mathcal{U}([0,1])$ and solve $F(x,\xi_t)=\zeta$ for $x$ \(\begin{align*} F(x,\xi_t)=\zeta & \Leftrightarrow 1-e^{-\xi_tx}=\zeta \\ &\Leftrightarrow e^{-\xi_tx} = 1-\zeta \\ &\Leftrightarrow \xi_tx = -\ln(1-\zeta) \\ &\Leftrightarrow \boxed{x = \frac{-\ln(1-\zeta)}{\xi_t}} \end{align*}\)

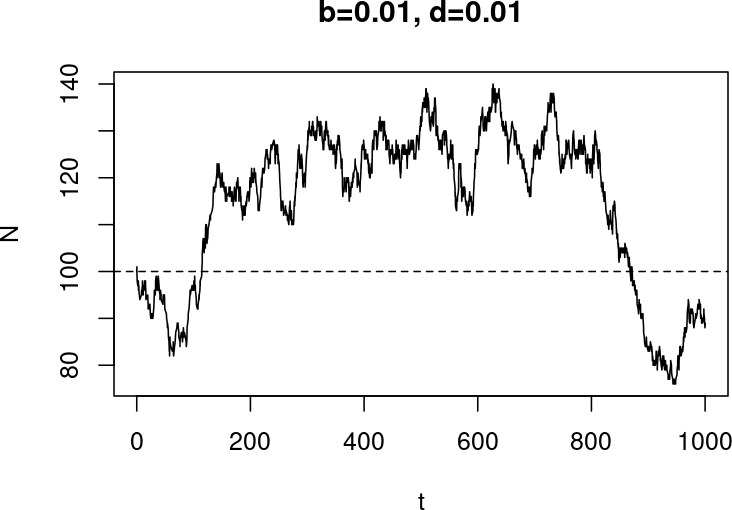
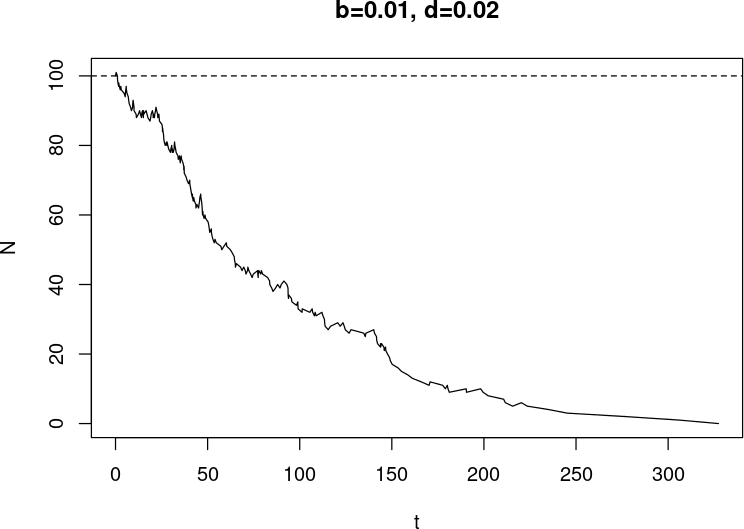
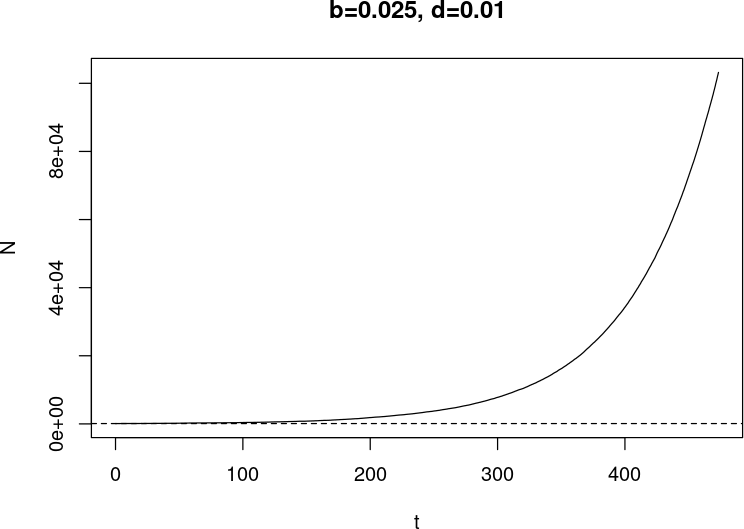
bg contain

bg contain

bg contain

Last one did not go well

bg contain

Tau-leaping to the rescue!