Petit cours d’épidémiologie mathématique
Types de modèles stochastiques utilisés en épidémiologie

Julien Arino

Department of Mathematics & Data Science Nexus University of Manitoba*

Centre canadien de modélisation des maladies (CCDM/CCMM) NSERC-PHAC EID Modelling Consortium (CANMOD, MfPH, OMNI/RÉUNIS)

* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.

---

Plan de ce cours

• Motivation de la stochasticité
• Quels types de systèmes stochastiques ?

---

Remarque - Remerciement

Certains des transparents ici sont inspirés de transparents que Linda Allen (Texas Tech) m’a donné il y a quelques années. Je recommende les livres et articles de Linda pour plus de détails

---

Motivation de la stochasticité

---

Modèle SIS sans démographie

Population totale constante $P^\star$

Nombre de reproduction élémentaire: \(\mathcal{R}_0 = \dfrac{\beta}{\gamma}P^\star\)

---

Dans le monde déterministe, $\mathcal{R}_0$ fait la loi

• Si $\mathcal{R}_0=\beta P^\star/\gamma<1$, la maladie s’éteint (ESM)
• Si $\mathcal{R}_0>1$, la maladie converge vers un équilibre endémique \(I^\star=P^\star-\gamma/\beta=(1-1/\mathcal{R}_0)P^\star\)

Transparents suivants: $P^\star = 100$K, $\gamma=1/5$, $\mathcal{R}_0={0.8,1.5,2.5}$ (et $\beta=\gamma \mathcal{R}_0/P^\star$)

---

---

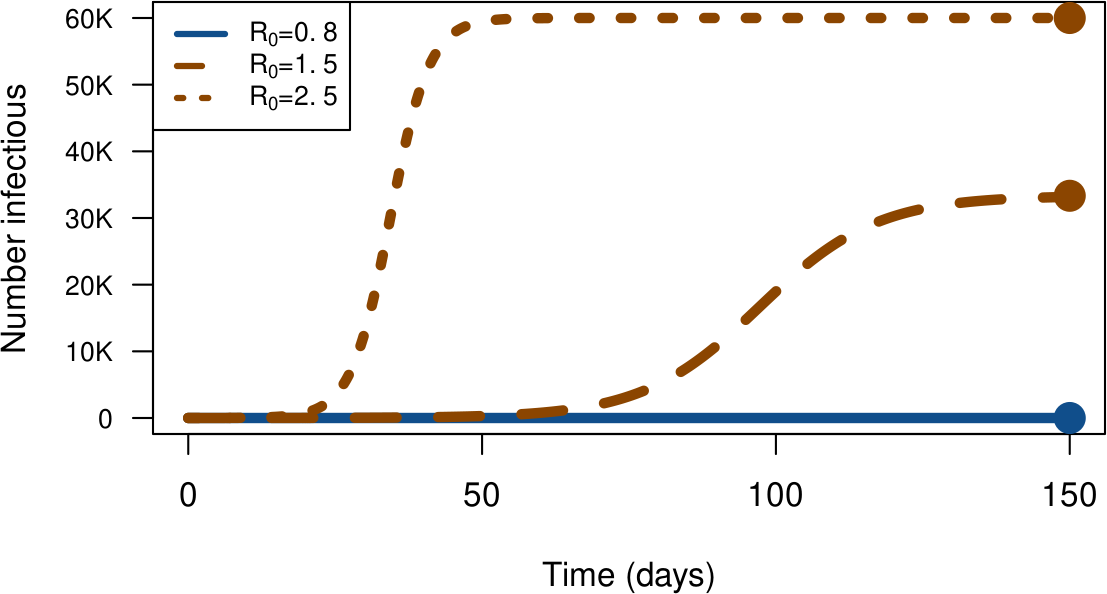
Dans le monde stochastique, $\mathcal{R}_0$ fait la loi ? ($\mathcal{R}_0=1.5$)

---

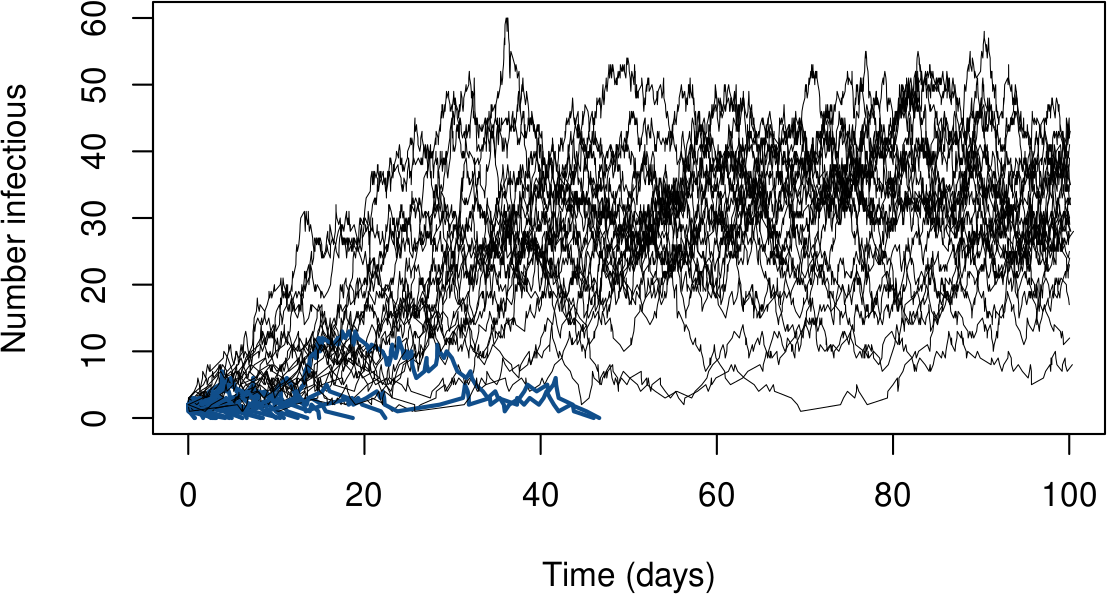
Lorsque $I_0=2$, les extinctions arrivent assez fréquemment

---

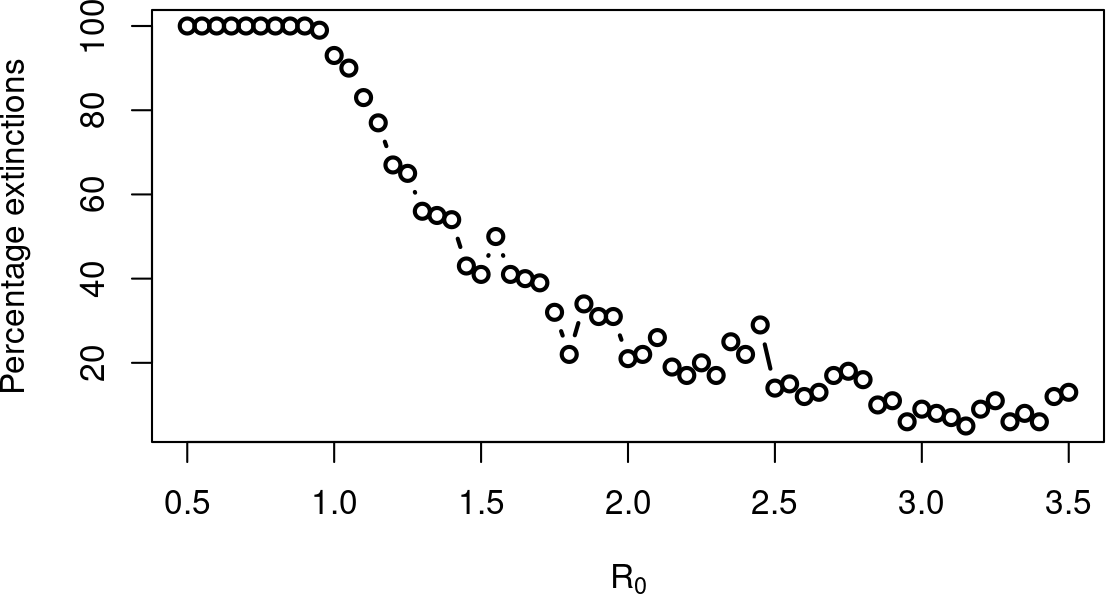
Quels types de systèmes stochastiques ?

---

Modèles de chaines binomiales

• Modèle de Reed-Frost (circa 1920)
  • Infection propagée des individus I vers les autres après contact approprié
  • Tout individu S, après contact avec un individu I dans une période donnée, développe une infection et est infectieux pour les autres seulement dans la période de temps suivante; dans la période suivante, devient R
  • Chaque individu a une probabilité donnée d’entrer en contact avec n’importe quel autre individu dans le groupe par intervalle de temps, et cette probabilité est la même pour tout membre du groupe
  • Population close
• Nombreuses variations et améliorations depuis

---

Chaînes de Markov en temps discret (CMTD)

• Présenté en détail dans le Cours 15 et, numériquement, le Cours 16
• Équivalent des systèmes en temps discret mais incluent de la stochasticité
• Saut vers le prochain état dépend seulement de l’état actuel (le système n’a pas de mémoire)
• Facile à étudier en utilisant l’algèbre linéaire

---

Chaînes de Markov en temps continu (CMTC)

• Équivalent stochastique presque exact des EDO
• Conversion des ODE vers les CMTC et vice-versa très simple pour les modèles compartimentaux
• Plus difficiles à étudier que les CMTD mais quand même assez faciles

---

Processus de branchement

• Cas particulier des CMTC

---

Équations différentielles stochastiques

• Je vais confesser un certain biais contre les EDS: EDO avec du bruit ajouté, pas grand chose de plus